Exam 2

Math 378

Spring 2003

1-8 Prove or find a counter example. Do one of each pair of questions. Circle the one you will be proving.

1) The cube of any odd integer is odd.

2) The product of any two consecutive integers is even.

Proof of 1)

Wlogwma n is an odd integer. Thus by definition n = 2k + 1 for some integer k. Therefore by substitution Multiplying out the right hand side and simplifying we have . But is an integer since it is the sum and product of integers. Let j be the integer . Then by substitution Therefore by the definition of odd we may conclude that n3 is odd.

QED

Proof of 2)

Wlogwma n and n +1 are two particular but arbitrarily chosen consecutive integers. Either n is even or n is odd.

Case 1: n is even. By definition, since n is even, n = 2k for some integer k. Therefore by substitution n(n+1) = 2k(2k+1). Using algebra to simplify we see that
n(n+1) = 2(2k2 + k). But 2k2 + k is an integer since k is an integer. Let j be the integer 2k2 + k. Thus by substitution n(n+1) = 2j. Therefore n(n+1) is even by the definition of even.

Case 2: n is odd. By definition, since n is odd, n = 2k+1 for some integer k. Therefore by substitution Using algebra to simplify we see that But is an integer since k is an integer. Let j be the integer . Then by substitution n(n + 1) = 2j. Therefore n(n + 1) is even by the definition of even.

QED.

 

 

 

 

 

3) For all integers a and b, if a| b then a2 | b2.

4) The square root of an irrational number is irrational.

Proof of 3)

Suppose a and b are integers and a|b. [We must show a2|b2 ]. By definition of divides since a|b we know that b = a× k for some integer k. By squaring both sides of this equation we obtain b2= a2× k2. But k2 is an integer since k is an integer. Therefore
b2 = a2× (an integer). Thus by definition of "divides" we see that a2|b2.

QED

Proof of 4) (by contradiction).

Wlogwma x is an irrational number. Suppose the statement is false. Suppose is a rational number [and look for a contradiction]. Since is a rational number we know that by definition for some integers a and b where b ¹ 0. Squaring both sides of this equation yields . But a2 and b2 are integers since a and b are integers and
b2 ¹ 0 since b ¹ 0. Thus x is a rational number by definition since it has been written as the ratio of two integers and the denominator is not equal to zero. This contradicts the premise that x is an irrational number. Therefore is an irrational number.

QED

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5) For all odd integers n,

6) For all real numbers x,

 

Proof of 5)

Wlogwma n is an odd integer. Hence by definition n = 2k +1 for some integer k. By substituting and simplifying. But k < k + 1/2 < k + 1, and k and k +1 are consecutive integers. Therefore by definition of ceiling . Combining the two equalities we see . But n = 2k +1 so . Substituting this into the last equality and simplifying we see . QED.

 

Proof of 6)

This statement is false!

Counterexample: Let x = 3/2. Then x2 = 9/4, , and . Thus in this case. Hence the statement is false.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7) Given any two distinct rational numbers r and s with r < s, there is a rational number x such that r < x < s.

8) There is no least positive rational number.

Proof of 7)

Wlogwma r and s are rational numbers and r < s. By definition we know for some integers a, b, c, and d with b ¹ 0 and d ¹ 0. Consider the number . By substituting and simplifying 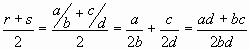. Now ad + bc and 2bd are both integers since they are the sum and products of integers. Also 2bd ¹ 0 since neither b nor d is zero. Therefore we may conclude that is a rational number since it has been written as the ratio of two integers where the denominator is not equal to zero. [It only remains to be shown that ].

Since r < s we know r + r < s + r. Therefore 2r < r + s. Dividing by 2 we see . Similarly since r < s we know r + s < s + s. Therefore r + s < 2s and . By combining these two inequalities we see . Let , then x is a rational number such that r < x < s. QED

 

Proof of 8) (by contradiction)

Assume there is a least positive rational number r. Since r is rational for some integers a and b with b ¹ 0. Now consider . Substituting we see . But a and 2b are integers since a and b are integers, and 2b ¹ 0 since b ¹ 0. Therefore is a rational number. Since 0 < r we may add r to both sides to obtain r < 2r. Combining these inequalities we have 0 < r < 2r. Dividing this last inequality by 2 we obtain . Therefore we have a contradiction, r cannot be the least positive rational number since is a positive rational number less than r. QED.

 

 

 

 

9 and 10 Use induction:

9) , for all integers n ³ 1.

 

Proof: (by Mathematical Induction).

Basis step: We must first show that the formula is true for n = 1. But when n = 1 the left hand side of the equation is and the right hand side is . Therefore the statement is true in this case.

Inductive step: [We must show if for some integer , then ]. Wlogwma that for some integer [This is the inductive hypothesis]. Now consider . By making the second to last term explicit we see . Using the inductive hypothesis to substitute into the left had side of this equation we see . Using algebra to simplify the left hand side of the equation we see . The left hand simplifies even further to . Finally factoring and canceling on the left hand side we obtain . QED.

 

 

 

 

 

 

 

10) Suppose b0, b1, b2, b3, … is as sequence defined as follows:

b0=2,

b1=1,

bk=bk-1+2bk-2 for all integers k ³ 2.

Prove that for all integers n ³ 0.

Proof: (by mathematical induction)

Basis Step: [Show the property holds for n = 0 and n = 1]

When n = 0, the L.H.S is 2 and the R.H.S. is 20 + (-1)0=1 +1 =2. Therefore the statement is true in this case. When n = 1 the L.H. S. is 1 and the R.H.S. is 21 + (-1)1 = 2 - 1 = 1. Therefore the statement is also true in this case.

Inductive Step: [We must show that given an integer k ³ 2, if for all j with , then ]. Wlogwma for all j with [this is the inductive hypothesis]. Since k ³ 2 we know k - 1 ³ 1 and k - 2 ³ 0. Therefore the inductive hypothesis may be applied to bk-1 and bk-2. Hence and . By definition bk=bk-1+2bk-2. Substituting in for bk-1 and bk-2 we see that . Using algebra to simplify we see that . But since (-1)2 = 1 we know . Therefore . QED.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

11) Suppose n is an integer such that

a) Does 23 have to divide n? Why or why not?

Yes. The number 23 is a prime and a factor of the right hand side. By the unique factorization theorem it must be a factor of the left hand side also. Since 23 is not a factor of 2, 3, 4, or 5 it must be a factor of n.

 

 

12) Write the following in product notation.

=

 

 

13) Assume you were going to prove the statement for all integers n ³ 2 using weak induction.

a) What would be your basis step? Do it.

We must show that the statement is true for n = 2. When n = 2 the left hand side is 8 and the right hand side is 5. Since 8 > 5 the statement is true in this case.

 

b) What would be your inductive step?

We must show that if for some integer k ³ 2, then

 

 

14) Suppose you were going to prove the following statement by contraposition.

"If the sum of two real numbers is less than 100 then at least one of the numbers is less than 50." What statement would you actually try to prove?

If two numbers are both greater than or equal to 50 then their sum is greater than or equal to 100.